Lesson 8: Nash Equilibrium
Beneath the Surface
In just about one year, spanning roughly from the spring of 1989 to the spring of 1990, Leninist regimes that had monopolized political power in several Eastern European countries for several decades up to that point were overthrown by popular revolutions. Each of these revolutions featured sudden outbreaks of street protests in which thousands of residents defied the ruling regimes’ bans on public expression of political opposition. To the astonishment of everyone at the time, including many of the protesters themselves, these mass revolts were successful. In one country after another, attacks on the crowds by police and security services, if there were any at all, were too feeble to stop the protests. At that point, regime leaders realized that they no longer had sufficient coercive force to govern, and conceded power to rival elites who in turn set up new political institutions.
In a 1991 study, Timur Kuran (1991) points out a puzzling feature of the Eastern European revolutions: In retrospect, the revolutions seem inevitable and perfectly explainable. “In each of the six countries” in which the revolutions occurred, he writes, “the leadership was generally despised, lofty economic promises remained unfulfilled, and freedoms taken for granted elsewhere existed only on paper.” “But,” he asks, “if revolution was indeed inevitable, why was it not forseen?” (Kuran 1991, 12) In fact, none of the experts on the region, nor any of the political elites in the region itself seem to have anticipated that a revolution would occur at the moment it did. Evidently, then, the conditions in those six countries that were visible to everyone at the time – e.g. widespread discontent in their populations, obvious failures of economic policy, etc. – cannot by themselves have been the causes of the revolutions. Indeed, those conditions had been present and obvious to everyone for decades during which no revolutions occurred! Whatever triggered the 1989 revolutions, then, was something beneath the surface, difficult or impossible to observe until after it had already emerged.
Kuran uses a game-theoretic model to depict a process through which a change in a population that is invisible from outside the population triggers the sudden outbreak of mass political protest. Here is a simplified version of Kuran’s model that partially illustrates the ideas he develops:
Imagine a population of N persons, where N is some very large positive integer. Suppose these persons live in a nation ruled by a regime that all of them would like to see overthrown. Suppose further that all are aware that if a very large portion of the population simultaneously participate in street protests, the regime will fall. However, for each person, the choice of whether to participate in any such protest is fraught. Each person knows that if only a small fraction of the population participates in a protest, the protest will be too small to overthrow the regime and the (few) persons who participate in the protest are all likely to be jailed or killed for doing so. On the other hand, if somehow a large fraction of the population participate in a protest, the protest will be so large that the regime’s security services will be overwhelmed, and the regime will fall. All this means that each person’s willingness to participate in a street protest depends on her expectation about the proportion of other persons in the population who will participate.
We can depict this situation using a simultaneous move game in which the persons are the N persons in the population. In this game, each of the N persons chooses between one of two available actions: to participate in a protest or to not participate in a protest. Further, the utility level that each person gets at any profile of actions depends on (a) whether that person participates in the protest in that profile, (b) the proportion of the N persons who participate in that profile and (c) a number T greater than 0 and less than or equal to 1 that we’ll call the population’s “threshold”. Specifically, take any one person in the population, and any one profile of actions in which the proportion of the population participating in the protest is any given proportion P. Then that person’s payoff at that profile of actions is: \left\{ \begin{array}{ll} 1 & \text{if that person participates and $P \geq T$;} \\ 1 & \text{if that person does not participate and $P < T$;} \\ 0 & \text{otherwise.} \end{array} \right\}
This payoff function captures the basic idea that each person’s preferences about whether not to participate in protest depend on whether she expects a sufficiently large portion of the population other than herself to participate. You can see this in two steps. First, imagine a person who expects that a relatively small fraction of the persons other than herself will participate in a protest. More precisely, suppose she expects that a number k of the N-1 persons in the population other than herself will participate in protest and that \frac{k+1}{N} < T, where T is the population’s threshold. Then, that person will expect that if she participates, the total proportion of the population participating will be P = \frac{k+1}{N} and if she does not participate the total portion will be P = \frac{k}{N}. Either way, P < T, and so she expects to get utility level 1 from not participating and 0 from participating. Thus she prefers to not participate instead of participate.
Now imagine the same person expects a relatively large fraction of the persons other than herself will participate in a protest. More precisely, suppose she expects that a number k of the N-1 persons in the population other than herself will participate in protest and that \frac{k}{N} \geq T, where T is the population’s threshold. Then, that person will expect that if she participates, the total proportion of the population participating will be P = \frac{k+1}{N} and if she does not participate the total portion will be P = \frac{k}{N}. Either way, P \geq T, and so she expects to get utility level 1 from participating and 0 from not participating. Thus she prefers to participate instead of not participate.
So far, nothing introduced in this model is different from anything presented in Lesson 7. This is simply a simultaneous move game depicting strategic interdependence between the N persons in the population. Specifically, it depicts each person’s preferences over her actions (to participate or to not participate) as depending on the actions she expects all the other persons to take.
But to use this model (as Kuran uses his more elaborate model) to depict either mass quiescence, on the one hand, or mass protest, on the other, and to explain why the shift from the former to the latter might be surprising, we need to introduce an additional concept: Nash Equilibrium. You’ll learn the precise technical definition of Nash Equilibrium in the subsequent sections of this lesson. For the purpose of the model here, however, think of a Nash Equilibrium as a profile of actions in which each person’s action is the best one for her if she correctly expects that every other person will act as in that profile.
For instance, in the model above, one Nash Equilibrium is the profile in which every one of the N persons in the population participate in protest. You can think of this profile as one in which each person’s action is the best action for her if she correctly expects that every other person will act as in that profile. Why? If any one person expects that every other person will participate, then she will expect that if she also participates, the proportion of the population participating will be P = 1. This proportion is necessarily at least as large as the threshold T. Thus this person will expect that if she participates she will get her maximum possible utility of 1 – i.e. participating will be a best action for her. Thus if she participates and every other person also participates, she will be taking the action that is best for her given an expectation about what everyone else does that turns out to be correct.
With this example of a Nash Equilibrium in mind, recall the puzzle this model is meant to make sense of: What changes in a population would be invisible when they occur and (yet) could cause a sudden and surprising mass uprising? The model here sheds light on this because two of its profiles of actions are each Nash Equilibria. The first of these is the one described in the previous paragraph in which every person in the population participates in protest. You can think of that profile as depicting a mass uprising that results in revolution. The other is the profile in which every one of the N persons does not participate. You can think of that profile as depicting mass quiescence, resembling the decades of political stasis that preceded the revolutions of 1989. Mass quiescence – i.e. the profile in which none of the N persons participate in protest – is a Nash Equilibrium in this game because if any one person expects that every other person will not participate, then she will expect that if she also does not participate, the proportion of the population participating will be P = 0. This proportion is necessarily smaller than the threshold T. Thus this person will expect that if she does not participate she will get her maximum possible utility of 1 – i.e. not participating will be the best action for her. Thus if she does not participate and every other person also does not participate, she will be taking an action that is best for her given an expectation about what everyone else does that happens to turn out to be correct.
So this model can depict two completely different patterns of behavior by the population – a mass revolt in which the entire population turns out for a protest, and mass quiescence in which no one turns out at all. Moreover, these two patterns of behavior can each be interpreted (since they are Nash Equilibria) as arising from widely-shared and correct expectations about what each person in the population will do. If everyone expects no one else to participate in a protest, then everyone will find it in her best interest to not participate and thus no one will participate, and thus everyone’s expectations will be correct. On the other hand if everyone expects everyone else to participate in a protest, then everyone will find it in her best interest to participate and thus everyone will participate, and thus everyone’s expectations will be correct.
This suggests an invisible change that can trigger a mass change in visible behavior: What persons in a population expect each other to do is generally invisible to those outside the population. But what those person actually do is visible. And, in this model, large and widespread changes the expectations persons in the population have about one another’s behavior can trigger tremendous shifts in actual behavior. Thus the model suggests how mass revolts can break out suddenly and unexpectedly: Something causes a shift in large portions of the population’s expectations about how their fellow citizens will act. Such a shift in expectations, when it happens, will be invisible, but can trigger a very visible outbreak of mass unrest.
Best Responses
In this lesson, you’ll learn how to identify Nash Equilibria in simultaneous-move games with two players. As a first step, you’ll master the concept of a best response. The concept of a best response applies in any simultaneous move game, regardless of the number of players and regardless of the number actions from which each player chooses. But it is easiest to master by first exploring its application to games in which there are two persons who each choose from three available actions.
To depict games with two persons who each have three actions we’ll use the same matrix form conventions you learned in Lesson 7. For instance, here is the matrix form of a game with two persons who each have three actions:

The payoffs in the cells of the matrix above are ordered according to the same convention used in the matrix form for 2-by-2 games. Specifically, in each cell the row-person’s payoff from the profile corresponding to that cell is listed first and the column person’s payoff is listed second. For instance, in the following matrix form, at the profile in which the “Row Person” takes the “middle” action and the “Column Person” takes the “right” action, the Row Person’s utility level is 1 and the Column Person’s utility level is 0:

With that in mind, suppose that the Row Person in this game expects the Column Person to take the “left” action. Examine the Row Person’s utility levels at each of the three profiles in which the Column Person takes the “left” action:
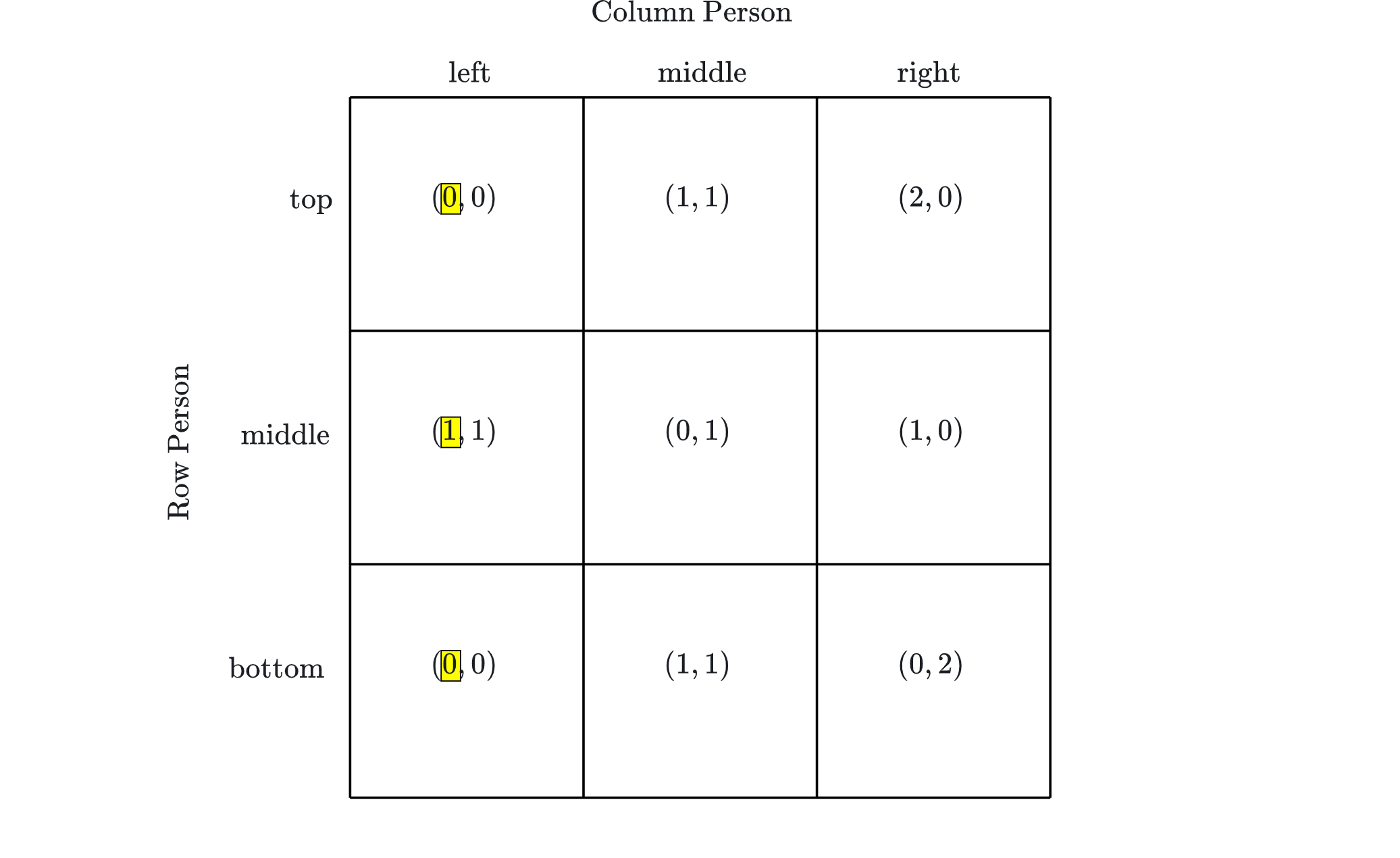
Observe that if the Row Person expects that the Column Person will take the left action, then she expects that there are two possible utility levels she can achieve depending on the action she takes: 0 and 1. More specifically, she expects that if she takes either the top or the bottom action her utility level will be 0, and if she takes the middle action her utility level will be 1. Thus, if the Row Person expects that the Column Person will take the left action, she will expect that she will get her highest possible utility level by taking the middle action. In that sense, the middle action is a best response for the Row Person to the expectation that the Column Person will take the left action. It looks like this:

The concept of a “best response” has a subtle feature that you should make sure not to miss: Multiple actions can each be best responses to a given expectation. For instance, suppose the Column Person in the game below expects the Row Person to take the middle action. Then the Column Person will expect that she will get utility level 1 from the left action, utility level 1 from the middle action and utility level 0 from the right action, like so:
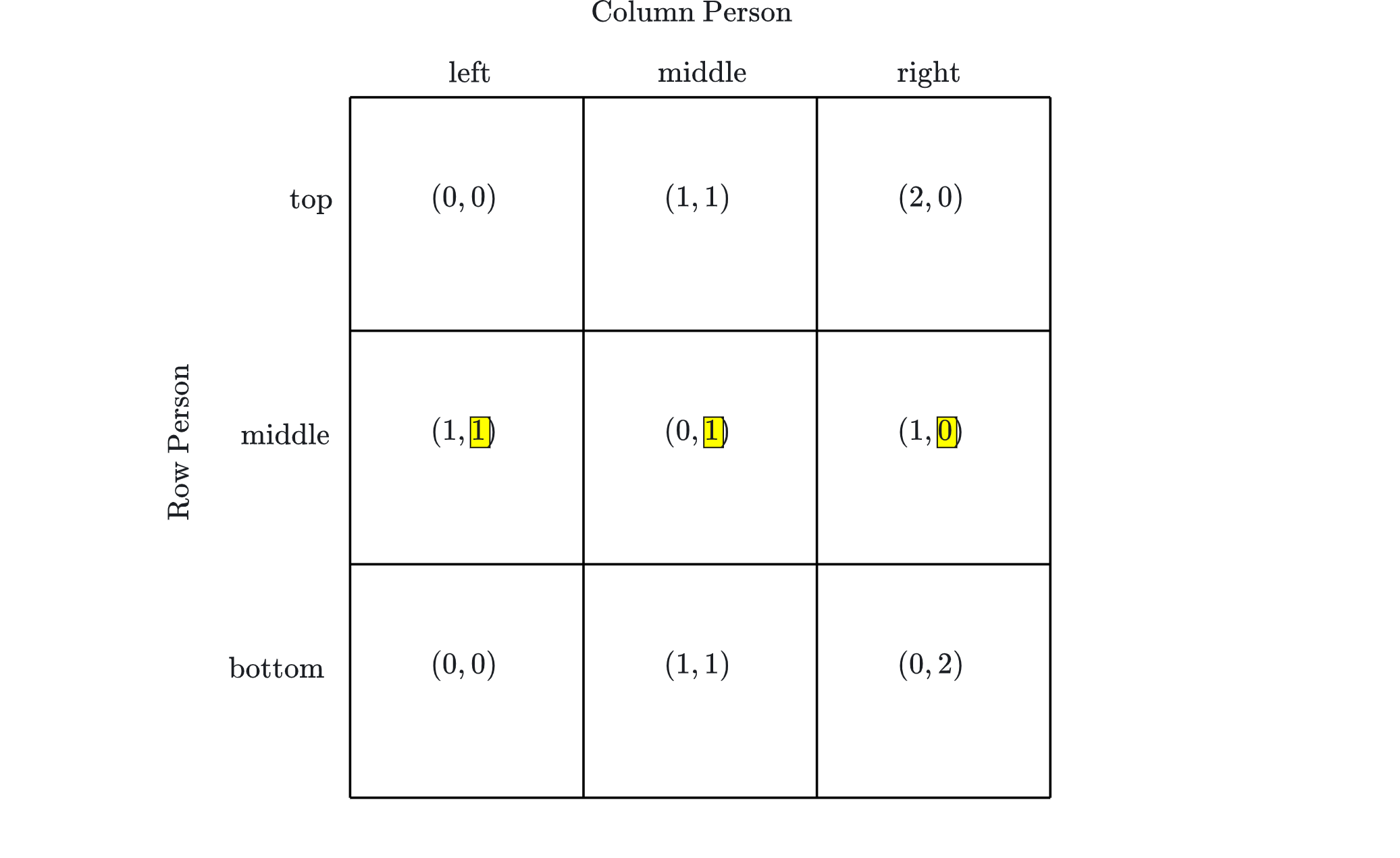
Examine the matrix above and notice that the highest utility level that the Column Person gets from any profile in which the Row Person takes the middle action is 1. Further, notice that when the Row Person takes the middle action, the Column Person gets that highest utility level of 1 when she takes either the left action or the middle action. Therefore, the left action and the middle action are each best responses for the Column Person to the expectation that the row person will take the middle action.
Pause and complete check of understanding 1 now!
Pause and complete check of understanding 2 now!
Nash Equilibrium
A Nash Equilibrium amounts to a profile of mutual best responses. More precisely:
For instance, in the following two-by-two game, the profile (\text{top},\text{left}) is a Nash Equilibrium:

To see this, first notice that if the Row Person expects the Column Person to take action “left”, then the Row Person expects to get utility level 1 by taking action “top” and utility level 0 by taking action “bottom”. Thus “top” is a best response by the Row Person to the expectation that the Column Person will take action “left”:

Now observe that if the Column Person expects the Row Person to take action “top”, then the Column Person expects to the get utility level 1 by taking action “left” and utility level 0 by taking action “right”. Thus “left” is a best response by the Column Person to the expectation that the Row Person will take action “top”:

Pause and complete check of understanding 3 now!
Pause and complete check of understanding 4 now!