COU 2: Nuclear Weapons are Scary, Part 1

The prospect of two nations that both have nuclear weapons going to war with one another is frightening. While it seems possible in principle that two nuclear-armed powers might mutually refrain from using nuclear weapons through the entire course of an armed conflict, it is easy to imagine why leaders of either of two nuclear-armed nations at war with one another might decide that use of nuclear weapons against the enemy is necessary.

To understand why, it helps to know how nuclear weapons, when used against a nation’s military forces, lines of supply or industrial or civil infrastructure, can affect that nation’s ability to continue to apply effective nuclear and non-nuclear military force to defend its interests. In short, nuclear weapons are so overwhelmingly powerful that they can instantaneously degrade or even eliminate a nation’s ability to defend itself. For instance, strikes by multiple nuclear weapons can, in the right circumstances, destroy most of a nation’s ground forces and its nuclear forces all at once. Thus, when two nuclear-armed nations are at war with one another, the leaders of each nation know that a nuclear strike by the adversary could suddenly degrade their military power, rendering them helpless to counter further aggression by the enemy. Even worse, the only way for either nation to eliminate it’s vulnerability to nuclear attack is a massive “first strike” with nuclear weapons intended to destroy most of the enemy’s nuclear forces before they can be used. Both nations in such a conflict, then, might decide at any time that a nuclear strike against the enemy is necessary for survival.

A Model of Nuclear Escalation

Here’s a simultaneous move game depicting the incentives that leaders of each of two nuclear-armed nations might have to use or not use nuclear weapons when those two nations are at war with each other. The game depicts two leaders: Leader A and Leader B who each command their nation’s nuclear and non-nuclear armed forces. It depicts a moment during the war in which each leader chooses from one of three actions: to refrain from a nuclear strike against the enemy, to order a limited nuclear strike, or to order a massive nuclear strike. Thus the matrix form of the game looks like this:

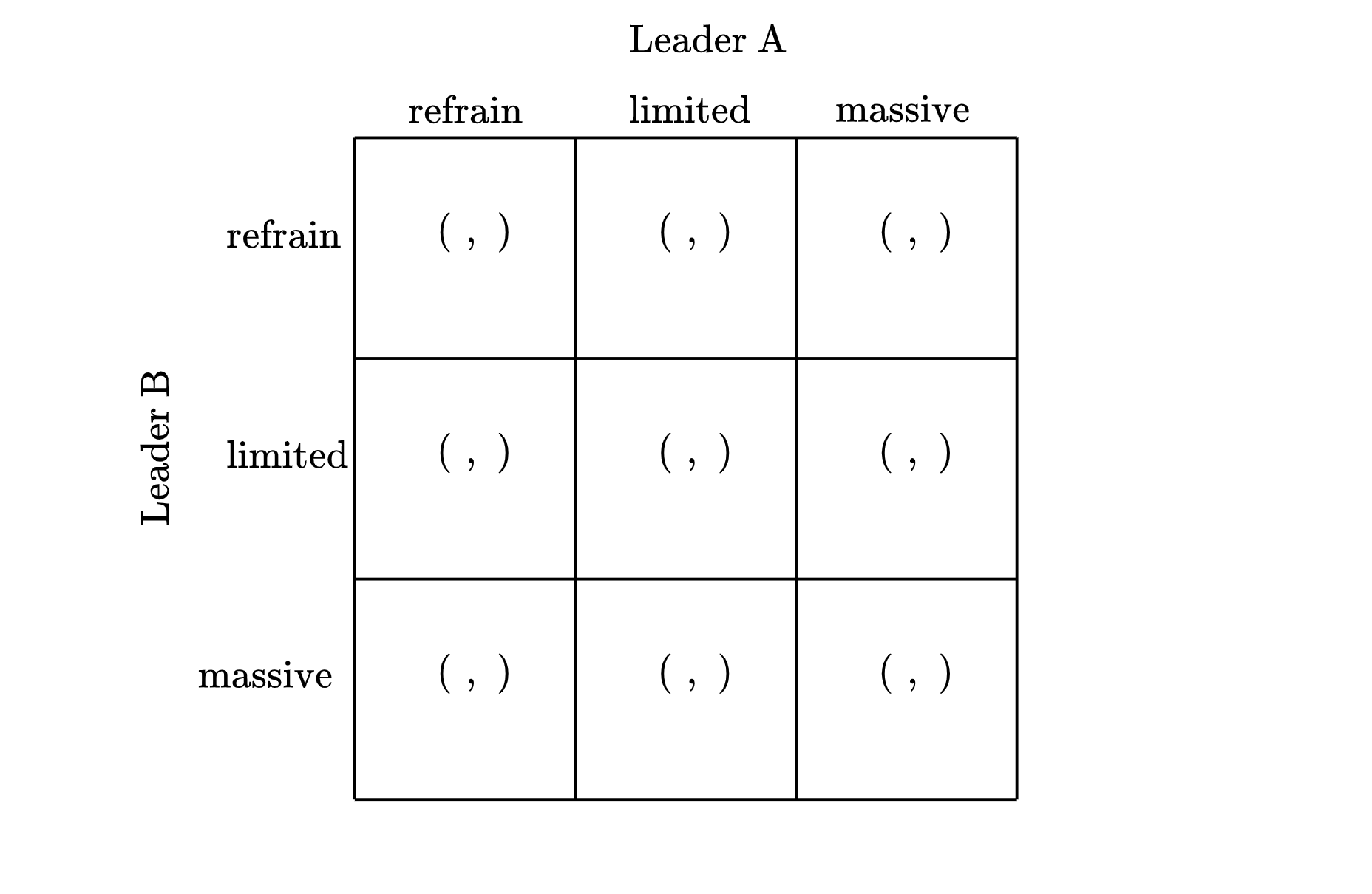
To depict the leaders’ incentives, we’ll start by assigning payoffs to the profiles along the diagonal of the matrix in which both leaders simultaneously take the same action. We’ll assume bilateral limited nuclear strikes make both leaders worse off than they would be if both refrained from nuclear use, and that bilateral massive nuclear strikes make them worse off still as follows:

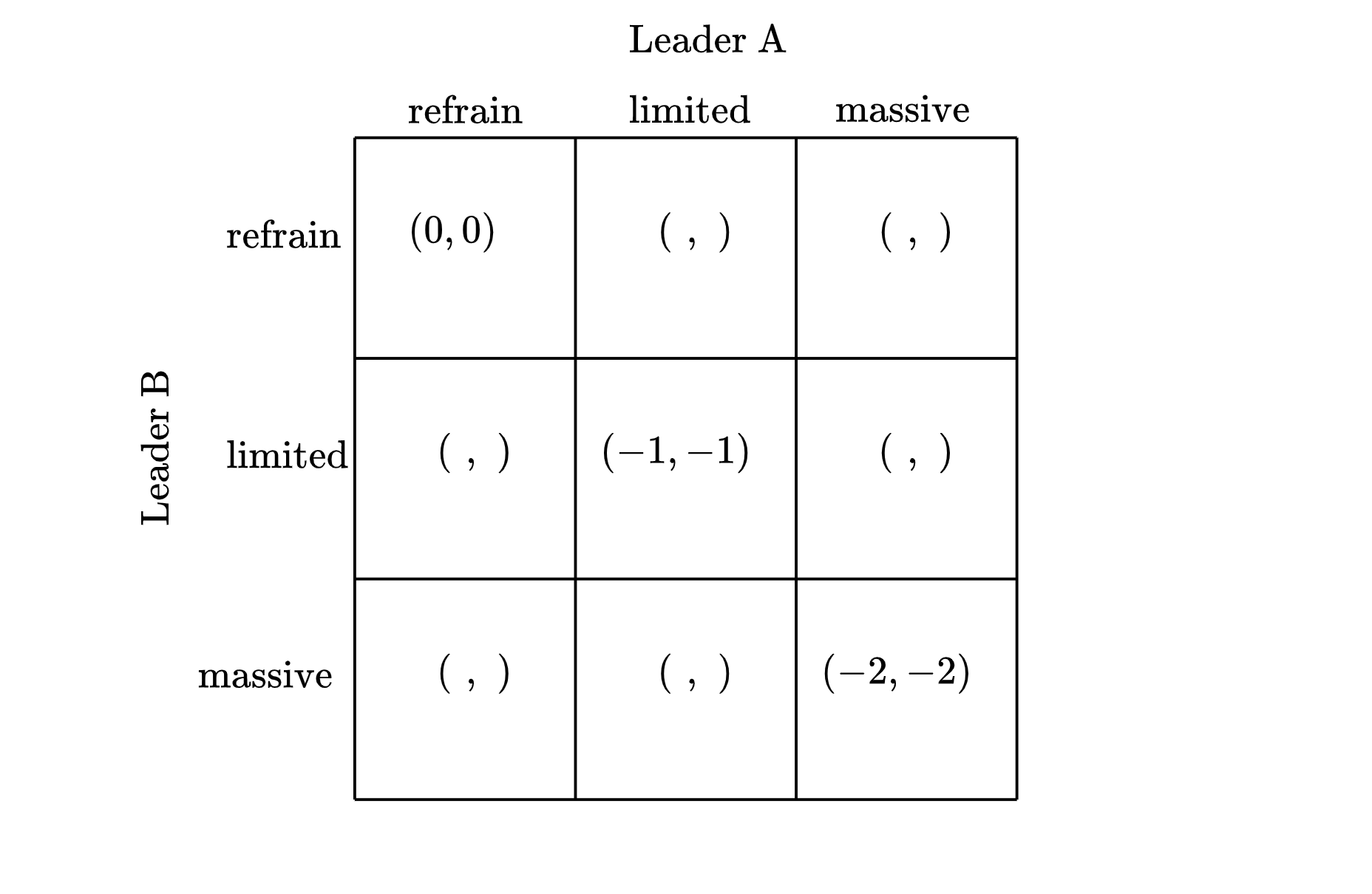
So far so bad. Now let’s depict how a leader is affected when she refrains from nuclear use but her adversary strikes unilaterally, and when a leader orders a limited nuclear strike while her adversary orders a massive strike. Because a nuclear strike on one’s nation by one’s enemy substantially degrades one’s ability to fight going forward, we’ll assume that when a leader’s nation is attacked by a nuclear strike and does not also attack with a strike of equal magnitude, the outcome is worse for the leader than any nuclear exchange in which both sides use the same amount of force. Specifically, if Leader A refrains from a nuclear strike while her adversary orders a limited or massive strike, or Leader A orders a limited strike while her adversary orders a massive strike, we’ll assume Leader A’s utility levels will be as follows:

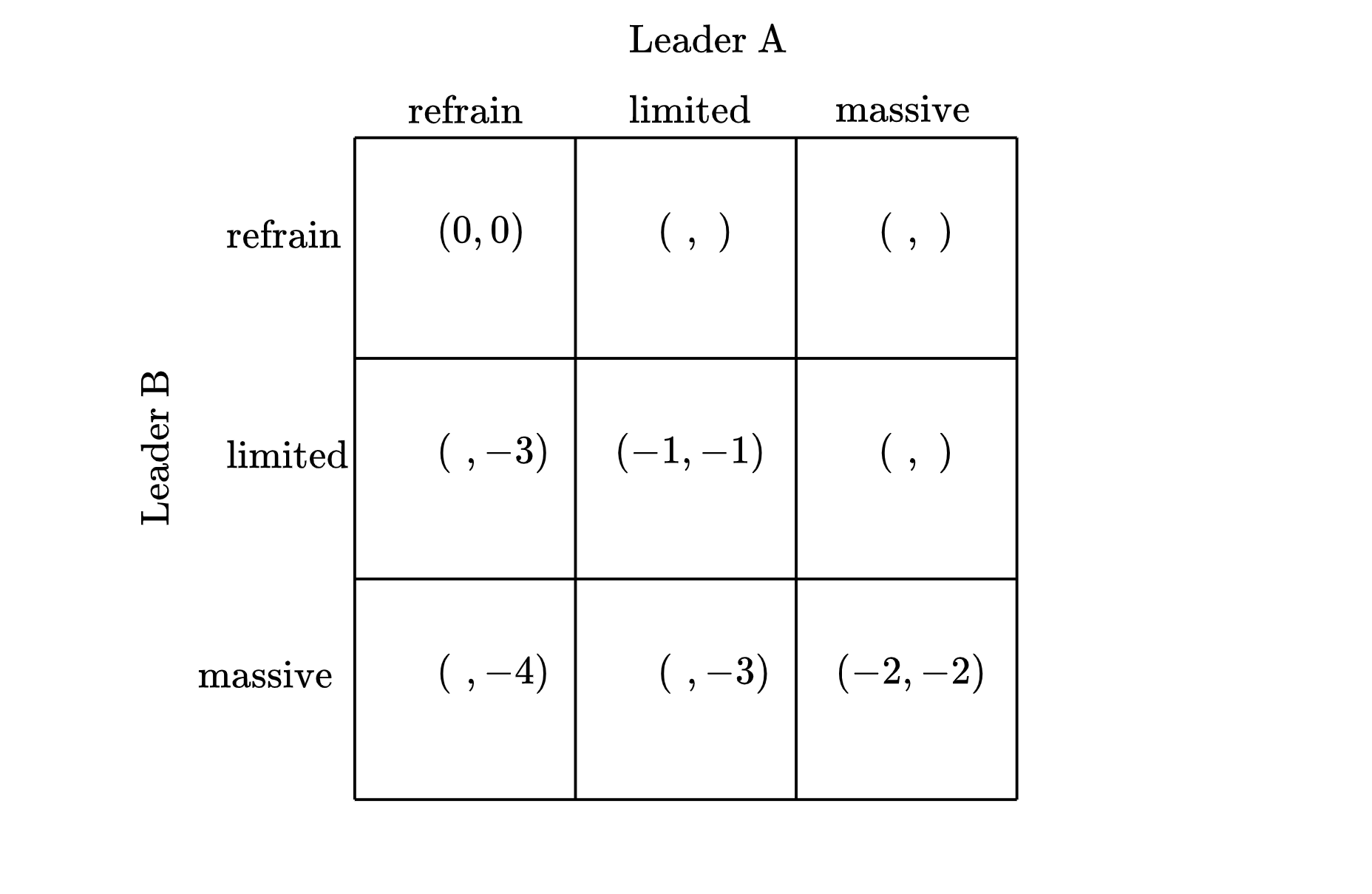
And we’ll assume a similar patter for Leader B:

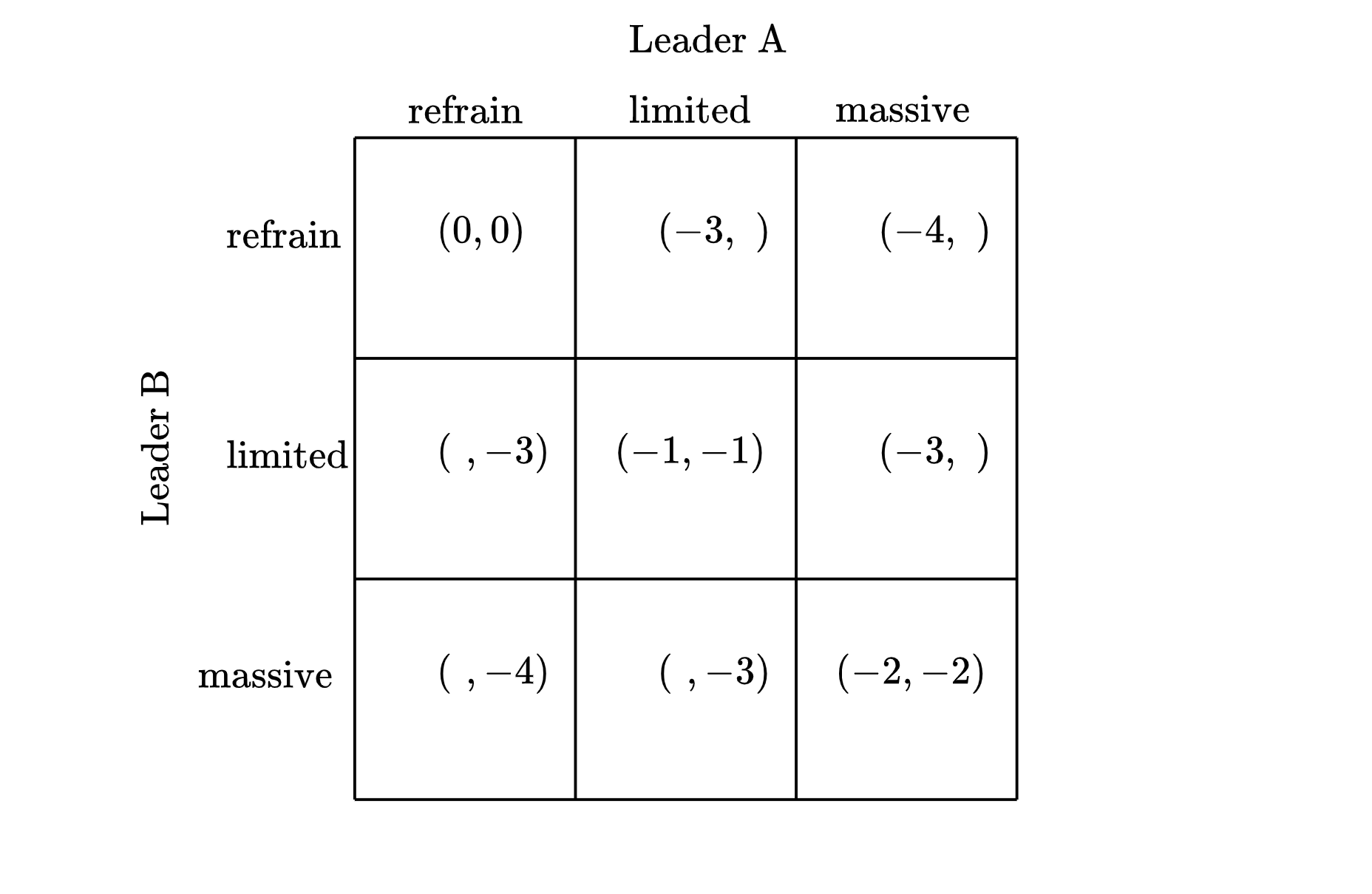
A Scary Implication

Even though the above matrix does not specify utility levels for both persons at every profile of actions, it produces a scary implication. To see this implication, respond to Prompts 1 and 2 below:

Prompt 1

Given the payoffs assigned in the (incomplete) matrix form above, what is Leader A’s best response to the expectation that Leader B will order a massive nuclear strike?

Prompt 2

Explain how you know the answer to Prompt 1 by stating the utility levels Leader A gets from each of the profiles in which Leader B orders a massive strike, stating the highest utility level that Leader A can get when Leader B takes orders a massive strike, and stating which of Leader A’s actions result in that highest utility level for Leader A when Leader B orders a massive strike.

A Ray of Hope?

Troubling as it is, the correct answer to Prompt 1 still leaves some room for hope. After all, it does not tell us what either leader might prefer to do if she expects her counterpart to refrain from ordering a nuclear strike. Try to imagine how and why a nuclear exchange might be avoided entirely by answering the following prompts.

Prompt 3

Re-write the matrix form of the game just as it appears immediately before Prompt 1, with the payoffs partially filled in. Then, fill in utility levels for Leader A at (i) the profile in which Leader A orders a limited strike and Leader B refrains from ordering a strike and (ii) the profile in which Leader A orders a massive strike and Leader B refrains from ordering a strike. The utility levels you fill in must be ordered relative to one another and relative to the utility levels already in the matrix so that Leader A’s only best response to the expectation that Leader B will refrain from ordering a strike is to refrain from ordering a strike.

Prompt 4

Explain why the utility levels you added to the matrix in response to Prompt 3 imply that Leader A’s only best response to the expectation that Leader B will refrain from ordering a strike is to refrain from ordering a strike by (i) stating the utility levels Leader A gets from each of the profiles in which Leader B refrains from ordering a strike, stating the highest utility level that Leader A can get when Leader B refrains from ordering a strike, and stating which of Leader A’s actions result in that highest utility level for Leader A when Leader B refrains from ordering a strike.

Prompt 5

Re-write the matrix form of the game just as it appears immediately before Prompt 1, with the payoffs partially filled in. Then, fill in utility levels for Leader B at (i) the profile in which Leader B orders a limited strike and Leader A refrains from ordering a strike and (ii) the profile in which Leader B orders a massive strike and Leader A refrains from ordering a strike. The utility levels you fill in must be ordered relative to one another and relative to the utility levels already in the matrix so that Leader B’s only best response to the expectation that Leader A will refrain from ordering a strike is to refrain from ordering a strike.

Prompt 6

Explain why the utility levels you added to the matrix in response to Prompt 5 imply that Leader B’s only best response to the expectation that Leader A will refrain from ordering a strike is to refrain from ordering a strike by (i) stating the utility levels Leader B gets from each of the profiles in which Leader A refrains from ordering a strike, stating the highest utility level that Leader B can get when Leader A refrains from ordering a strike, and stating which of Leader B’s actions result in that highest utility level for Leader B when Leader A refrains from ordering a strike.

Prompt 7

If you answered Prompts 3 and 5 correctly, you have shown that it is possible to imagine incentives for the two leaders that make it so that if each expects the other to refrain from a nuclear strike, each finds it in her interest to refrain from a strike as well. Great job! But what reasons do we have to believe that such incentives might occur? In introducing this model, we explained that when two nations are at war, either nation can render the other militarily defenseless through a nuclear strike. If two nuclear-armed nations are at war, then, why would the leader of either nation, expecting the other nation to refrain from a strike, not order a nuclear strike on her adversary? After all, by doing so she could win the war outright. The alternative is a long, costly and at-best-partially-decisive non-nuclear war – one which could escalate into a nuclear exchange at any point! In up to one-half a page of double spaced text, give reasons why, despite its potentially overwhelming military effectiveness, a leader of a nation at war might not find it in her interest to order a nuclear strike against her adversary when she expects that her adversary will not order one against her.

Rubric

Prompts 1 and 2 are scored exactly in the similarly-worded prompts in COU 1.

Prompts 3 and 5 are each worth 1 point. An answer gets one point if it fills in payoffs in the correct places in the matrix that are ordered as required in the prompt. It gets 0 points otherwise. No partial credit is available.

Credit is available on Prompt 4 only if Prompt 3 scores 1 point. If Prompt 3 DOES score 1 point, then Prompt 4 is scored exactly as the similarly-worded prompts in COU 1.

Credit is available on Prompt 6 only if Prompt 5 scores 1 point. If Prompt 5 DOES score 1 point, then Prompt 6 is scored exactly as the similarly-worded prompts in COU 1.

Prompt 7 gets 3 points if it is sufficiently free of grammar, spelling and usage errors and sufficiently legible to be easily understandable and it gives reasons for believing that a nuclear-armed nation at war will not conduct a first nuclear strike despite the overwhelming military advantages it might win by doing so. It scores 0 points otherwise, with no partial credit available.